Az "S" görbe

Úgy döntöttem, hogy júliusban egy kicsit szünetet tartok az eddigi nagy olvasási tempóban – részben a kiégés ellenszereként, részben változatosságnak, részben némi “nyaralás” ürügyén. De ettől a blog természetesen nem marad friss tartalom nélkül! Szabadjára engedem ugyanis a belső matekos, kocka énemet, és a következő hetekben a kedvenc grafikonjaimat (illetve a belőlük levonható tanulságokat) szeretném megosztani Veletek. És igen, tényleg ennyire szánalmas vagyok, hogy vannak kedvenc grafikonjaim.

Mai alanyunk az ún. “S” görbe, amiről először Jacob Lund Fisker könyvében olvastam – csak hát az akkori összefoglalóm ez a téma nélkül is két részbe fért csak bele, úgyhogy gondoltam majd máskor külön visszatérünk rá. És habár ez a konkrét modell újdonság volt, az alkotóelemei nem, hiszen az “S” görbe két nagyon fontos jelenséget egyesít: az exponenciális növekedést és a csökkenő megtérülést. Lássuk hát előbb ezeket az összetevőket, utána pedig a kombinációjukra is kitérhetünk.

Az exponenciális növekedés

Az exponenciális növekedés (avagy egyik gyakori álnevén, a “kamatos kamat”) sokak szerint a világ 8. csodája. Pszichológiai szemszögből azonban járhat bizonyos kellemetlen mellékhatásokkal, amikre jó előre felkészülni. Kezdjünk rögtön egy illusztrációval, hogy aztán azon keresztül (remélem) könnyebben megemészthessük a fogalmakat. Balról jobbra telik az idő, lentről felfelé pedig “haladunk”, jelentsen az bármit is.

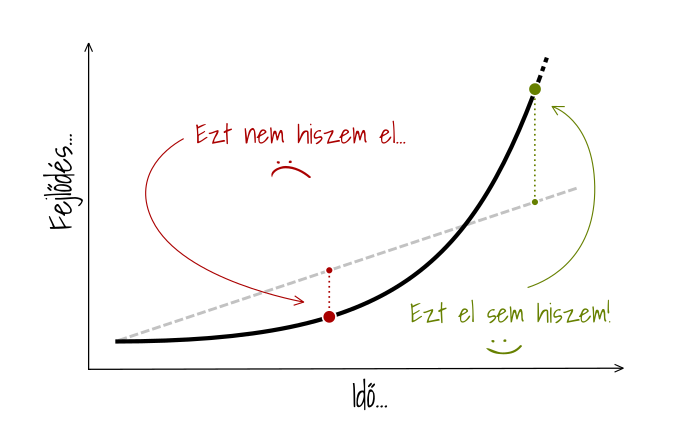
Az exponenciális változásra (vagyis a központi, vastag, íves, fekete vonalra) érdemes tehát úgy gondolni, hogy nem csak haladunk, de a tetejébe idővel egyre gyorsabban haladunk. Tesszük ezt szemben a lineáris változással (szürke, szaggatott vonal), ahol haladnánk ugyan, de mindig ugyanolyan tempóban. Amit viszont sokan nem vesznek figyelembe az exponenciális esetben, hogy az egyre gyorsuló növekedésnek először nyilván viszonylag lassan kell indulnia, hogy onnan aztán felgyorsulhasson.

Az ember agya alapvetően lineáris összefüggéseket vár el: amennyi munkát befektetünk, azzal egyenesen arányos eredményt is szeretnénk látni. Ez ezért baj, mert a fejlődés (egy darabig legalábbis) sokkal inkább exponenciális. És habár hosszú távon az exponenciális függvény az egyértelmű nyertes, rövid távon a lassú beindulás elveheti az ember kedvét az egésztől – márpedig ha ráhagyjuk, akkor nem is lesz hosszú táv.

Vegyük a pirossal jelölt időpontot. Itt a lineáris hozzáállásunk miatt azt várnánk, hogy már a magasabban lévő pici piros pöttynél leszünk, de sajnos a valóságban még csak a vaskosabb lentinél tartunk. Ilyenkor úgy érezzük majd, hogy hiába pazaroljuk azt a sok energiát, ez nekünk egyszerűen nem megy. Pedig megy az, csak az exponenciális pályát követve.

Ha viszont kitartunk, és szorgosan tesszük egyik lábunkat a másik után, egy idő után átbillen a mérleg – és onnantól meg már nem is akarunk majd hinni a szemünknek. A zöld időpontban például úgy fogjuk érezni, hogy még csak a lenti kicsi pöttynél kéne lennünk, de igazából már nagyon nem ott leszünk.

Összességében persze semmivel nem fogunk gyorsabban haladni attól, hogy a háttérben megbújó exponenciális összefüggéssel tisztában vagyunk. De attól talán megmenthetjük magunkat, hogy idő előtt feladjuk az erőfeszítést – és így eljuthatunk abba a bizonyos felszálló ágba, aminek reményében az egészbe belekezdtünk.

A csökkenő megtérülés

A csökkenő megtérülés, avagy a csökkenő hozadék (eredetileg “diminishing returns”) elve azt mondja ki, hogy a beletett munka egy bizonyos ponton túl már nem arányos a kinyert profittal. Ha ezt ábrázolni szeretnénk, akkor az eredmény tulajdonképpen a fenti görbe inverze. Mondhatjuk úgy is, hogy megfelelően sok idő után már kb. “fordítottan exponenciális” a haladás, és ezért aránytalanul sok energiát kell befektetnünk, hogy csak egy kicsit is feljebb juthassunk.

Illusztrációként láthatjuk, hogy a zöld pötty már eleve magasról indul. Persze először idáig is el kellett jutni (lásd az előző szekciót); de most legyünk jóindulatúak, és feltételezzük, hogy ez a kezdőpont. Ha viszont még innen is feljebb szeretnénk jutni, ahhoz a balról-jobbra irányban igencsak meg kell lódulnunk. És még ha meg is lódulunk, akkor sem haladhatunk olyan sokat felfelé, mint amennyit jobbra vagyunk kénytelenek.

Jogosan merülhet fel, hogy jogos-e ilyenkor is tovább “erőltetni” az adott területet. És persze, az olimpikonoknak, a sakk nagymestereknek, és a Guinness rekordtartóknak még ilyen feltételek mellett is megéri az üzlet. De nekünk többieknek érdemes elgondolkodni…

Itt jön a képbe a generalista szemlélet, ami szerint ilyenkor inkább vágjunk valami újba (ahol majd újra látványos haladásokat érhetünk el), míg az eredeti területet elég lesz “csak” szinten tartani. Ha az összesített tudásmennyiségünk maximalizálása a cél, akkor legyünk inkább kompetensek 10 dologban, mint vérprofik egyben, és teljesen bénák a maradék kilencben. És ne aggódjunk, van bőven elég ismeret a világon, hogy jó pár emberöltőt is eltölthetnénk unatkozás nélkül.

Az “S” görbe

Ennyi alapozás után pedig végre rátérhetünk a címadó “S görbére”, ami egy zseniálisan tömör mentális modell, hiszen gyakorlatilag a fenti két jelenség együttes ábrázolása. Ha egymás után fűzzük az exponenciális növekedés és a csökkenő megtérülés görbéit, akkor egy szép S betűszerű alakot kapunk:

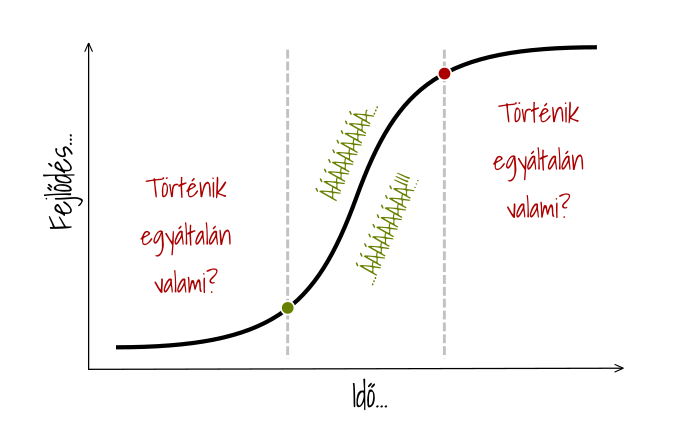
Az ábrán szürke szaggatott vonalakkal illusztráltam a két határt, amiket képesnek kell lennünk beazonosítani a hatékony fejlődés érdekében. Az első a zöld ponttal jelölt “áttörés”, ahol igazán beindul a szekér. Ezt persze könnyű észrevenni, ha már ott tart az ember; de annál nehezebb előre hinni benne, amikor még nem tartunk ott, és nem is nagyon látjuk, hogy hogyan tarthatnánk valaha ott.

Ehhez adhat plusz motivációt az exponenciális fázis ismerete. Amíg az áttörésig el nem jutunk, addig csak “Kuss, és lapátolj tovább!” Vagyis: mindenbe tegyük bele az energiát az elején, és (ami szinte még fontosabb) tartsunk ki odáig, ahol már majd “igazi” eredményeket láthatunk cserébe.

Viszont tudjuk megítélni azt is, hogy mikor “merítettük ki” a terület lehetőségeit – ezt jelöli a piros pont. Nyilván lehetnek kivételek, de sokunknak innentől hatékonyabb lesz a hajszálnyi extra fejlődés helyett valami más után nézni. És persze ne feledjük, hogy ha valami más után nézünk, akkor ott újra indul az “S” görbe! Attól, hogy egy hegyet már megmásztunk, attól a következő hegynél továbbra is lentről indul az expedíció.

A lényeg, hogy soha ne számítsunk lineáris haladásra. Képzeljünk egy “S” alakot az egyenes haladás helyére, és sokkal pontosabban fogjuk majd tudni, hogy hol tartunk. És hogy miért. És hogy ott mit is kellene csinálni.